sword_smith    2024-08-10 👍 1 👎

Hi Hunter!

Good job getting started on the Futhark programming and implementing hash_pair in Futhark!

We’ve tried running just the low-degree extension on a graphics card, and although we got a 3x speedup on the number theoretic transform (NTT) algorithm compared to running it on a CPU, we did not get an overall speedup because it also costs some time to send data to and from the GPU.

That lead us to the conclusion that we need to do more of the proving on the GPU in order to get a speedup. Luckily, we have a profile of the proof generator, so we can see which steps take a long time. The ultimate goal is eventually to port all of Triton VM (or at least all of the function that generates the STARK proof) to something that can run on a GPU, Futhark being a great candidate for this. But an intermediate goal is to just be able to get some speedup from the GPU.

To achieve this, I would suggest to attempt to run all LDE and all Merkle tree building on the GPU and see if this would yield a speedup. It’s possible that all steps from the 1st LDE to the end of the prover will have to run on a GPU – we’ll have to see. But to build a Merkle tree with Futhark, you definitely need to implement Tip5’s hash_varlen. Maybe that could be a next step?

I don’t think you need to implement BFieldCodec, as the encoding of the table rows (that are the arguments to hash_verlen) is just an array of b-field elements. In other words, the only encode implementations you need is that of an array of B-field elements and an array of X-field elements, both of which are straight forward.

The low-degree extension logic can be found here. Under the hood it calls Polynomial::fast_coset_interpolate and Polyonomial::fast_coset_evaluate which can both be found in the twenty-first repo. They rely on NTT which is the finite-field version of fast Fourier transform.

aszepieniec    2024-08-16 👍 1 👎

What a great way to learn about STARKs and GPU programming and functional programming patterns. Hats off. I’ll be watching your progress with a keen eye. And please let us know what we can do to help, even if it’s just answering questions if you get stuck.

holindauer    2024-08-17 👍 👎 [op]

Thanks!

I do have some questions wrt to the logistics of benchmarking speed and RAM consumption for LDE and Merkle building.

First I’d like to ask about what process you’d suggest for how to go about incorporating the futhark version into current benchmarking strategies? As well, would you explain a bit more about the setup/implementation for the benchmarking readout that was sent by Throkil in the previous response?

Currently, I’ve been developing on my local machine by ensuring the correct output of individual function translations. Building up the logic from the bottom of the call stack, so to speak. This has been for the most part straightforward, with key difficulties being in translating paradigm specific constructs like Options into Futhark, which they are not natively supported.

I was told by Throkil that I might run into some issues with large proofs running out the memory on the GPU. And that you’d have some good tips about how to reduce RAM consumption, I’d love to here them.

holindauer    2024-08-18 👍 👎 [op]

Also, with respect to the control flow inside of master_table.rs, is my understanding correct that the MasterBaseTable is created first, filled, low degree extended, and merkle-ized. Then, the MasterExtTable is created from the MasterBaseTable, to which it is again low degree extended and merkle-ized. But with an important difference being that the MasterBaseTable utilizes BField elements and polynomials. Whereas the MasterExtTable works with XField elements and polynomials?

jfs    2024-08-19 👍 👎

That understanding of the data flow in master_table.rs is correct, yes. A depiction of the general flow of data in a STARK can be found here. Note that (a) Triton VM uses an improved STARK to the one in that picture, meaning that some details are different, and (b) the picture applies to the STARK of a different VM. However, the general sentiment is still up to date.

With regards to (a), here are the things I can immediately identify as being different in the STARK engine used in Triton VM:

• initials are deterministic, not sampled at random. This also has implications for terminals, which are needed in fewer places.
• The arithmetic intermediate representation (“AIR”) still has four parts, but those are slightly different. Because initials are deterministic, there is no need for a difference AIR anymore. We found it beneficial to have so-called “consistency constraints,” which are the new fourth part.
• The randomizer codewords are concatenated to the MasterExtTable, not the MasterBaseTable (in the picture, extension codewords and base codewords, respectively).
• Just before entering the FRI phase, the picture implies a non-linear pseudorandomly weighted sum using two red boxes. (Admittely, it’s difficult to gauge this meaning from the picture alone.) We’ve dropped the non-linearity of this random sum.

Point (b) only affects the content of the two orange boxes labeld “AET” and “XEAT”, but not the general flow of data. For example, Triton VM has neither an input nor an output table – it uses a different solution for the problem they are addressing – but introduces many more other tables.

jfs    2024-08-19 👍 👎

what process [would you] suggest for […] incorporating the futhark version into current benchmarking strategies?

Good question. I’m entirely unfamiliar with the tooling around futhark. The first option that comes to my mind (and this probably warrants further exploration) is to start a new crate which uses both the CPU implementation and your GPU implementation as dependencies, and write the benchmarks there.

good tips about how to reduce RAM consumption

RAM requirements are certainly something we are trying to bring down as we keep working on Triton VM. For now, the simplest way to keep it low is to only work with programs that generate a short trace, which mostly means programs that terminate after a short while. Of course, this has the big caveat that benchmarks might be unrealistic. What levels of RAM usage are you currently observing?

sword_smith    2024-08-19 👍 1 👎

good tips about how to reduce RAM consumption

It’s also worth noting that a strategy to reduce RAM consumption is already present in the Triton VM repository. If the should_cache boolean variable declared here is false, then the Merkle tree is built from just-in-time low-degree-extended codewords. If it’s true, then the low-degree-extended codewords are stored on the MasterTable struct. I think it would make sense to only cover the should_cache = false codepath in the Futhark code, as the other codepath is going to run out of RAM on any GPU for reasonably sized proofs.

holindauer    2024-08-22 👍 👎 [op]

Thank you, this was very helpful.

I have a quick update and a question.

Update:

At this stage, I have been working to implement the low_degree_extend_all_columnns() method for the MasterExtTable with the goal of developing a framework for performance benchmarks against the rust implementation once implemented.

I have implemented many of the functions of which low_degree_extend_all_columns() calls internally. I am at a point now where I am able to port the logic for the ‘polynomial zero-initialization’ and ‘interpolation’ steps.

To test my futhark implementation against that in rust, I attempted to write a function that would create test vectors for the MasterExtTable before and after LDE. However, I am running into some issues that I am not sure how to resolve.

The initial way I went about creating these test vectors was with the below function. It is a modification to the setup within the test “master_ext_table_mut()”. :

#[test]
fn low_degree_extend_all_columns_example() {

    let trace_domain = ArithmeticDomain::of_length(1 << 8).unwrap();
    let randomized_trace_domain = ArithmeticDomain::of_length(1 << 9).unwrap();
    let quotient_domain = ArithmeticDomain::of_length(1 << 10).unwrap();
    let fri_domain = ArithmeticDomain::of_length(1 << 11).unwrap();

    let randomized_trace_table =
        Array2::ones((randomized_trace_domain.length, NUM_EXT_COLUMNS));

    let mut master_table = MasterExtTable {
        num_trace_randomizers: 16,
        trace_domain,
        randomized_trace_domain,
        quotient_domain,
        fri_domain,
        randomized_trace_table,
        low_degree_extended_table: None,
        interpolation_polynomials: None,
    };

    println!("\nBefore low-degree extension:");
    println!("{:?}\n", master_table.randomized_trace_table);

    (&mut master_table).low_degree_extend_all_columns();

    println!("\nAfter low-degree extension:");
    println!("{:?}\n", master_table.randomized_trace_table);
}

The issue I ran into here was that the trace_column within the following portion of the low_degree_extend_all_columns() function would unwrap on a None value when attempting to represent as a slice.

    // compute interpolants
    profiler!(start "interpolation");
    Zip::from(self.randomized_trace_table().axis_iter(Axis(1)))
        .and(interpolation_polynomials.axis_iter_mut(Axis(0)))
        .par_for_each(|trace_column, poly| {
            let trace_column = trace_column.as_slice().unwrap();   // <------------- Unwraps on a None here
            let interpolation_polynomial = randomized_trace_domain.interpolate(trace_column);
            Array0::from_elem((), interpolation_polynomial).move_into(poly);
        });
    profiler!(stop "interpolation");

This made me think that perhaps the way I was setting up the master_table in that test didn’t make sense. And that the values within the table needed to come from an actual tasm program and could not be arbitrary.

Because of this, I began writing the following function that would run the stark prover all the way up to the LDE of the MasterExtTable. This test used the factorial program from the examples dir as the program:

#[test]
fn example_master_ext_table_lde(){

    // The program that is to be run in Triton VM. Written in Triton assembly.
    // The given example program computes the factorial of the public input.
    let program = triton_program!(
        // op stack:
        read_io 1           // n
        push 1              // n accumulator
        call factorial      // 0 accumulator!
        write_io 1          // 0
        halt

        factorial:          // n acc
            // if n == 0: return
            dup 1           // n acc n
            push 0 eq       // n acc n==0
            skiz            // n acc
            return      // 0 acc
            // else: multiply accumulator with n and recurse
            dup 1           // n acc n
            mul             // n acc·n
            swap 1          // acc·n n
            push -1 add     // acc·n n-1
            swap 1          // n-1 acc·n
            recurse
        );

    // Note that all arithmetic is in the prime field with 2^64 - 2^32 + 1 elements.
    // The `bfe!` macro is used to create elements of this field.
    let public_input = PublicInput::from([bfe!(1_000)]);

    // The execution of the factorial program is already fully determined by the public input.
    // Hence, in this case, there is no need for specifying non-determinism.
    let non_determinism = NonDeterminism::default();

    let (aet, public_output) = program.trace_execution(public_input.clone(), non_determinism).unwrap();

    let claim = Claim {
        program_digest: program.hash(),
        input: public_input.individual_tokens,
        output: public_output,
    };

    // The default parameters give a (conjectured) security level of 160 bits.
    let stark = Stark::default();

    // Generate the proof. 
    let proof = stark.prove_up_to_LDE(&claim, &aet).unwrap();  
}

The method stark.prove_up_to_LDE() is a modified version of stark.prove() that ends directly after the call of low_degree_extend_all_columns(). The issue I ran into with this function is that when the test from above calls self.derive_max_degree(padded_height), the program panics.

pub fn prove_up_to_LDE(
    &self,
    claim: &Claim,
    aet: &AlgebraicExecutionTrace,
) -> Result<bool, ProvingError> {
    // fiat-shamir claim
    let mut proof_stream = ProofStream::new();
    proof_stream.alter_fiat_shamir_state_with(claim);

    // derive additional parameters
    let padded_height = aet.padded_height();

    let max_degree = self.derive_max_degree(padded_height); // ! <--------- crashes here
    let fri = self.derive_fri(padded_height)?;
    let quotient_domain = Self::quotient_domain(fri.domain, max_degree)?;
    proof_stream.enqueue(ProofItem::Log2PaddedHeight(padded_height.ilog2()));

    // base tables
    let mut master_base_table =
        MasterBaseTable::new(aet, self.num_trace_randomizers, quotient_domain, fri.domain);

    // pad
    master_base_table.pad();

    // randomized trace
    master_base_table.randomize_trace();

    // LDE
    master_base_table.low_degree_extend_all_columns();

    // Merkle Tree
    let base_merkle_tree = master_base_table.merkle_tree();

    // Fiat Shamir
    proof_stream.enqueue(ProofItem::MerkleRoot(base_merkle_tree.root()));
    let challenges = proof_stream.sample_scalars(Challenges::SAMPLE_COUNT);
    let challenges = Challenges::new(challenges, claim);

    // extend 
    let mut master_ext_table = master_base_table.extend(&challenges);

    // ext tables
    master_ext_table.randomize_trace();

    // ext tables
    master_ext_table.low_degree_extend_all_columns();

    // TODO:fix return
    Ok(true)
}

The panic happens within constraints.rs on line 98:

fn initial_quotient_degree_bounds(_: isize) -> Vec<isize> {
    panic!("{ERROR_MESSAGE_GENERATE_DEGREE_BOUNDS}")  
}

I am a bit unsure about how to proceed from here. I think I may have a misunderstanding about what is required for the setup of low_degree_extend_all_columns. Is this approach to developing test vectors misinformed?

sword_smith    2024-08-24 👍 👎

Some of the code in the Triton VM repository is autogenerated. And when you clone from github the autogenerated code is not included.

To generate the autogenerated code, run this command in the root-directory of triton-vm:

cargo run --bin constraint-evaluation-generator

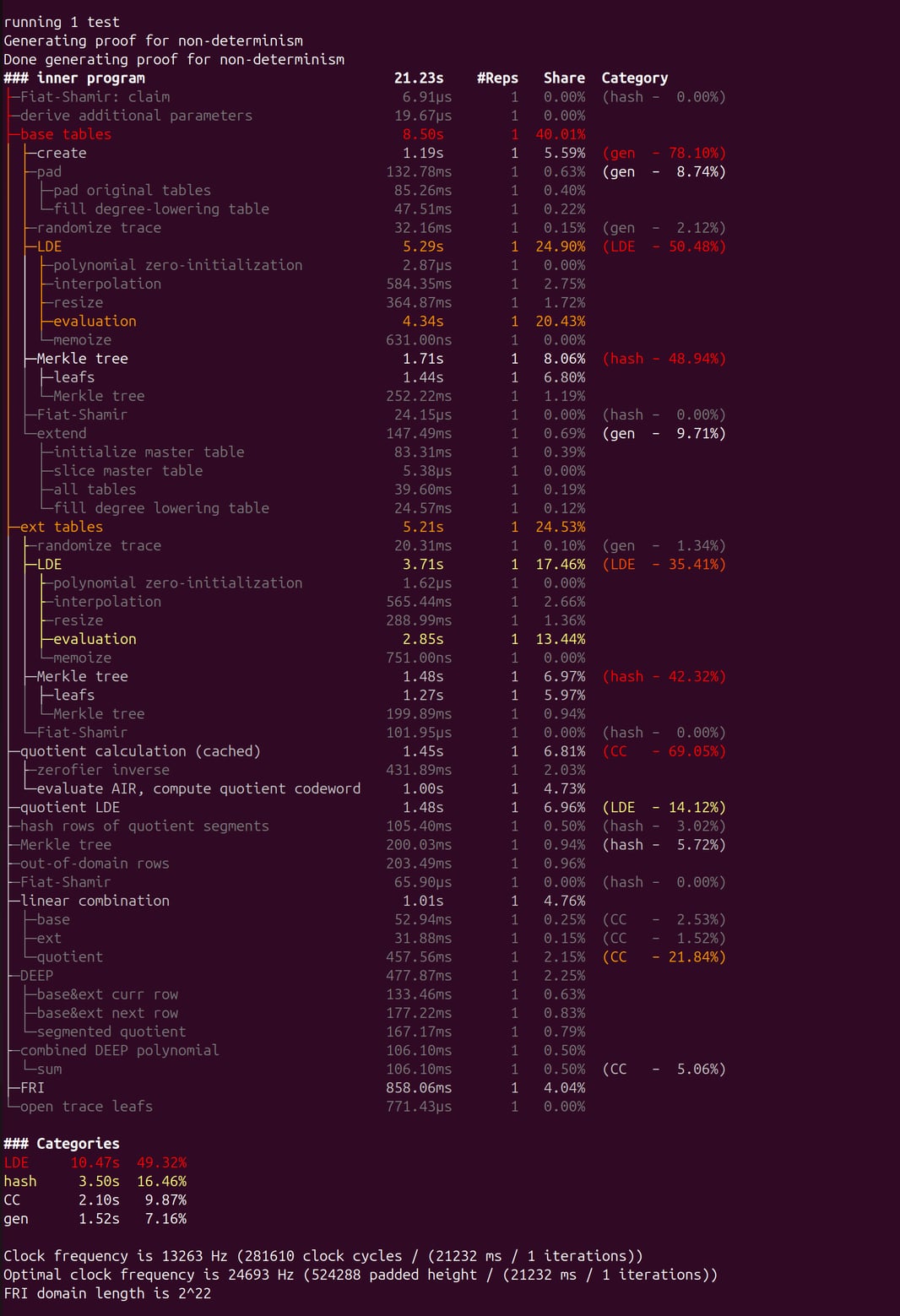
holindauer    2024-09-03 👍 2 👎 [op]

Hi, quick update:

As of yesterday, I was able to get .low_degree_extend_all_columns() for the MasterExtTable running on the GPU.

Initially it is much faster than running on the CPU. So far, I have done a few preliminary benchmarks to get a sense for this speedup using the factorial program from the triton-vm examples dir.

Here is a printout of some elapsed times for LDE on factorials of increasing powers of 2.

CPU: Factorial(2 ** 0): 0 s / 3 ms – randomize_trace_table dim: (512, 88) CPU: Factorial(2 ** 1): 0 s / 2 ms – randomize_trace_table dim: (512, 88) CPU: Factorial(2 ** 2): 0 s / 2 ms – randomize_trace_table dim: (512, 88) CPU: Factorial(2 ** 3): 0 s / 2 ms – randomize_trace_table dim: (512, 88) CPU: Factorial(2 ** 4): 0 s / 1 ms – randomize_trace_table dim: (512, 88) CPU: Factorial(2 ** 5): 0 s / 3 ms – randomize_trace_table dim: (1024, 88) CPU: Factorial(2 ** 6): 0 s / 5 ms – randomize_trace_table dim: (2048, 88) CPU: Factorial(2 ** 7): 0 s / 7 ms – randomize_trace_table dim: (4096, 88) CPU: Factorial(2 ** 8): 0 s / 13 ms – randomize_trace_table dim: (8192, 88)

Here is what the time becomes when running calling the futhark entry point for LDE on the GPU:

GPU: Factorial(2 ** 0): 0 s / 0 ms – randomize_trace_table dim: (512, 88) GPU: Factorial(2 ** 1): 0 s / 0 ms – randomize_trace_table dim: (512, 88) GPU: Factorial(2 ** 2): 0 s / 0 ms – randomize_trace_table dim: (512, 88) GPU: Factorial(2 ** 3): 0 s / 0 ms – randomize_trace_table dim: (512, 88) GPU: Factorial(2 ** 4): 0 s / 0 ms – randomize_trace_table dim: (512, 88) GPU: Factorial(2 ** 5): 0 s / 1 ms – randomize_trace_table dim: (1024, 88) GPU: Factorial(2 ** 6): 0 s / 1 ms – randomize_trace_table dim: (2048, 88) GPU: Factorial(2 ** 7): 0 s / 2 ms – randomize_trace_table dim: (4096, 88) GPU: Factorial(2 ** 8): 0 s / 4 ms – randomize_trace_table dim: (8192, 88)

After a factorial of >= (2 ** 9) I begin to run into issues regarding high memory consumption leading to an unsuccessful exit. I think a potential solution to this would be to run LDE for an amount of columns that does not exceed the threshold of individual XFieldElements within the factorial(2 ** 8) run.

For example, it would be something like this: On the rust side, gather chunks of randomized trace table columns that do not exceed a total count of (8192 * 88) XFieldElements. Run LDE on those select columns. Repeat step 1 and 2 for the rest of the table. Then assemble the outputs into the expected format I should also note that the GPU times above only include the time for running a futhark entry point from rust. They do not include the time it takes to convert rust types to the appropriate types needed to call within futhark.

A bit of context for those who are unfamiliar with this pipeline: In order to provide interop between rust and futhark, we are using a library called genfut. Genfut is used to generate a rust library with bindings to entry points in futhark code that has been compiled to Cuda/OpenCL/C.

The biggest bottleneck right now for the LDE accelerator is the time it takes to do these conversions for the randomized_trace_table. The futhark entry point accepts the randomized trace table as a 3d array of u64 (w/ the last dimension bound to 3: [][][3]u64 in futhark). Genfut represents this intermediary type as Array_u64_3d. On the rust side, before calling the entry point, the MasterExtTable.randomized_trace_table is converted from an Array2 to [][][3]u64. The return value, the interpolation polynomials from the LDE is converted from [][][3]u64 to Vec<Polynomial>.

The times with associated with these conversions times are listed here:

Conversion to genfut types: 0 s / 0 ms GPU: Factorial(2 ** 0): 0 s / 0 ms – randomize_trace_table dim: (512, 88) Conversion back to rust types: 0 s / 2 ms

Conversion to genfut types: 0 s / 0 ms GPU: Factorial(2 ** 1): 0 s / 0 ms – randomize_trace_table dim: (512, 88) Conversion back to rust types: 0 s / 1 ms

Conversion to genfut types: 0 s / 0 ms GPU: Factorial(2 ** 2): 0 s / 0 ms – randomize_trace_table dim: (512, 88) Conversion back to rust types: 0 s / 2 ms

Conversion to genfut types: 0 s / 0 ms GPU: Factorial(2 ** 3): 0 s / 0 ms – randomize_trace_table dim: (512, 88) Conversion back to rust types: 0 s / 1 ms

Conversion to genfut types: 0 s / 0 ms GPU: Factorial(2 ** 4): 0 s / 0 ms – randomize_trace_table dim: (512, 88) Conversion back to rust types: 0 s / 1 ms

Conversion to genfut types: 0 s / 1 ms GPU: Factorial(2 ** 5): 0 s / 1 ms – randomize_trace_table dim: (1024, 88) Conversion back to rust types: 0 s / 3 ms

Conversion to genfut types: 0 s / 2 ms GPU: Factorial(2 ** 6): 0 s / 2 ms – randomize_trace_table dim: (2048, 88) Conversion back to rust types: 0 s / 6 ms

Randomized Trace Table Conversion to Genfut Types: 0 s / 5 ms GPU: Factorial(2 ** 7): 0 s / 3 ms – randomize_trace_table dim: (4096, 88) Conversion back to rust types: 0 s / 13 ms

Conversion to genfut types: 0 s / 9 ms GPU: Factorial(2 ** 8): 0 s / 4 ms – randomize_trace_table dim: (8192, 88) Conversion back to rust types: 0 s / 25 ms

I think that this could be optimized primarily by reducing the amount of conversions that happened from rust to futhark.

My next immediate steps will probably be to work to update the Merkle Tree entry points from the original ruthark fork. I believe it was using a different hash function than Tip5. It shouldn’t be too bad to make that change.

Let me know your thoughts on the project at this stage and my suggested improvements.

Thankyou, -Hunter

sword_smith    2024-09-05 👍 👎

Hi Hunter!

Glad to see that there’s progress on the Futhark/GPU front. STARK proof generation is a very parallelizable operation, so GPUs are a good fit.

I see three challenges:

• data conversion times
• data transfer times
• RAM consumption on the GPU

The solution to the data conversion problem is to either do less conversion or to ensure that the RAM layout on the host-machine (CPU calculations) matches what the GPU code can work with.

The solution to the data transfer times is most likely to do more calculations on the GPU – to delegate to it a big part of the prover, not just individual steps but tying the individual steps together in GPU code.

And the solution to the RAM consumption is already addressed somewhat in the CPU code here, and here as you can either evaluate the entire FRI domain for all columns in one go, or you can evaluate it just-in-time and do the sponge absorption on chunks of the FRI domain as you evaluate the FRI-domain codeword from the interpolants.

It looks to me like you’re on the right path, though, as it’s probably a good idea to build all individual parts first and then string them together as the GPU code becomes increasingly more capable.

sword_smith    2024-09-05 👍 👎

Actually, the main motivation behind MasterExtTable was to ensure that the 1st challenge was addressed. So it shouldn’t be necessary to do data conversion before sending the table to the GPU. I think that should work.

A bit of historical context: Prior to MasterExtTable, we represented the tables in Rust as Vec<Vec<XFieldElement>>, and with that construction, the data will not live in a contiguous part of memory. With MasterExtTable it does.